রাত তখন অনেক গভীর, সবাই ঘুমিয়ে গেছে। একজন মানুষের কোনো ঘুম নেই। লম্বা একটা জোব্বা গায়ে, শশ্রুমন্ডিত লোকটি বেরিয়ে গেল ঘর থেকে। একটা লণ্ঠন একহাতে ধরে আরেক হাতে ধরেছে একটা গাঁইতি। গা ছমছমে পরিবেশে লোকটির যেনবা কোনোই ভয়-ডর নেই। সে গিয়ে ঢুকলো একটা কবরস্থানে। কোথাও ডেকে উঠলো একটা নিশাচর প্রাণী। গাঁইতি হাতে লোকটি, সদ্য কবর দেয়া একটা কবরে চলে গেল। খুড়তে শুরু করলো গাঁইতি দিয়ে। একসময় বেরিয়ে পড়লো কফিনটা। তারপর সেই কফিন থেকে লাশটা বের করে কাঁধে তুলে নিল লোকটা – একটুও ভয়-ডর নেই। লাশটাকে অন্ধকারে, চুপি চুপি নিয়ে এলো নিজের ঘরে। ঘরটায় যন্ত্রপাতি দিয়ে ঠাসা। মেঝেতে শুইয়ে রাখলো লাশটাকে। এবার আসল কাজ শুরু: লাশটাকে মেঝেতে বিছিয়ে রেখে লোকটি তার যন্ত্রপাতি নিয়ে শুরু করলো… কাটাছেঁড়া?? না, শুরু করলো জ্যামিতি।
ইতালির ভেনিসে, গ্যালারি দেল’এ্যাকাদেমিয়া-তে একটা চিত্রকর্মের সামনে দাঁড়িয়ে আছেন এক দর্শক। খুব অল্প সময়ের জন্য চিত্রকর্মটির প্রদর্শনী হচ্ছে বলে প্রচুর লোকের সমাগম হয়েছে চিত্রকর্মটি দেখার জন্য, তাই সে বেশিক্ষণ সময় পাবে না এই ছোট্ট চিত্রকর্মটির সামনে থাকার। তবু সে একবার তাকায় নিজের টি-শার্টের বুকে ছাপা করা ছবিটির দিকে, আরেকবার তাকায় সামনের হলদে পাতায় আঁকা চিত্রকর্মটির দিকে: ভিট্রুভিয়ান ম্যান।
মার্কাস ভিট্রুভিয়াস পোলিও (Marcus Vitruvius Pollio), প্রাচীন রোমের একজন স্থপতি। একটা বই লিখলেন তিনি, নাম “দে আর্কিতেকচুরা”। বিশাল বইটির তৃতীয় খন্ডে লিখলেন এক আশ্চর্য বিষয়: স্থাপত্যের আদি নীতির কেন্দ্রবিন্দু নাকি মানুষ। তিনি তাঁর বইতে বর্ণনা করলেন, মানুষ নাকি আশ্চর্য কিছু অনুপাতের মিশেল। তিনি এই অনুপাতগুলোকে স্থাপত্যের উপজীব্য হিসেবে ব্যাখ্যা করলেন।
বহু দূরে প্রায়ান্ধকার একটা কক্ষে এই বইটিই পড়ছিলেন একজন লোক। নাম তাঁর লিওনার্দো, ইতালির ভিঞ্চি গ্রামে জন্মগ্রহণ করায় তাঁকে সবাই ডাকে ভিঞ্চির লিওনার্দো, বা লিওনার্দো অফ ভিঞ্চি— লিওনার্দো দা ভিঞ্চি। আজব সব শখ ছিল তাঁর, তারই একটা ছিল কবর থেকে লাশ তুলে এনে পরীক্ষা-নিরীক্ষা করা। কখনও কাটাছেঁড়া করে শারীরবিজ্ঞান-রহস্যোদ্ঘাটন, কিংবা কখনও জ্যান্ত মানুষকে দিয়ে যেসব পরীক্ষা-নিরীক্ষা করা যায় না, সেসবের আয়োজন। বিচিত্র এই মানুষটি ভিট্রুভিয়াসের বইয়ে মানুষ সম্পর্কে লেখা সেই অনুপাতের বিষয়টি পড়ে দারুণ রোমাঞ্চিত হলেন। চিত্রকর মানুষ, মনের মাঝে সবকিছুই ছবির মতো ভাসে… তিনি ঠিক করলেন এই অনুপাতের বিষয়টিকে চিত্রে রূপ দিবেন। সালটা আনুমানিক ১৪৮৭ খ্রিস্টাব্দ, জন্ম হলো ভিট্রুভিয়ান ম্যান-এর।
লিওনার্দো সব সময় তাঁর সঙ্গে রাখতেন কিছু নোটবুক। সেসব নোটবুকে তিনি যেমন লিখতেন তাঁর গবেষণালব্ধ বিভিন্ন বিষয়, তেমনি আঁকতেন বহু বহু ছবি। কিন্তু লিখতেন বড় আশ্চর্য ভঙ্গিতে, ইতালীয় ভাষায়, সব উল্টো হরফে। ফলে নোটবুকের লেখার মর্মোদ্ধার করতে দরকার হবে আয়নার। তারই একটা পাতায় তিনি আঁকলেন এই চিত্রকর্মটি-
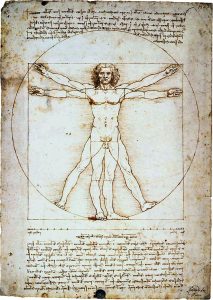
ছবিটিতে দেখা যায় একজন মানুষ, একটা বৃত্ত এবং একটা বর্গক্ষেত্রের মধ্যে খুব সাজুয্যপূর্ণভাবেই এঁটে যান। চলুন লিওনার্দো’র নোটবুক থেকেই এর ব্যাখ্যাটা শোনা যাক:
“… আপনি যদি আপনার পা-দুটো দুপাশে এমনভাবে ছড়ান, যাতে আপনার উচ্চতা ১/১৪[চৌদ্দ ভাগের এক ভাগ] কমে যাবে; এবং আপনার হাতদুটো দুই পাশে মেলে ধরেন, এমনভাবে যেন আপনার হাতের মধ্যমা আঙ্গুলটির ডগা ঠিক আপনার মাথার চূঁড়ার সমান হয়, তাহলে আপনার হাত দুটো আর পা দুটোর অবস্থানকে স্পর্শ করে পুরোপুরি একটা বৃত্ত আঁকা যাবে আর আপনার নাভি হবে সেই বৃত্তের কেন্দ্র; এই দুই পায়ের মাঝখানের ফাঁকটি হুবহু একটি সমবাহু ত্রিভুজ তৈরি করবে।” {“The Notebooks of Leonardo da Vinci” edited by Irma A. Richter}
এই বর্ণনাসহ নোটবুকে বর্ণিত লিওনার্দো’র অন্যান্য বর্ণনা ও চিত্রকর্ম থেকে যে বিষয়গুলো জানা যায়:
- দুদিকে সমানভাবে প্রসারিত হাতের এমাথা-ওমাথা মাপ আসলে ঐ মানুষটির উচ্চতা।
- চুলের গোড়া থেকে থুতনির নিচ পর্যন্ত দূরত্ব হলো একজন মানুষের সম্পূর্ণ উচ্চতার ১০ ভাগের ১ ভাগ।
- থুতনির নিচ থেকে মাথার অগ্রভাগ পর্যন্ত দূরত্ব হলো একজন মানুষের উচ্চতার ৮ ভাগের ১ ভাগ।
- বুকের উপর থেকে মাথার অগ্রভাগ পর্যন্ত দূরত্ব হলো উচ্চতার ৬ ভাগের ১ ভাগ
- বুকের উপর থেকে চুলের গোড়া পর্যন্ত দূরত্ব হলো উচ্চতার ৭ ভাগের ১ ভাগ
- কাঁধের সর্বোচ্চ দূরত্ব হলো উচ্চতার ৪ ভাগের ১ ভাগ
- স্তন থেকে মাথার অগ্রভাগ পর্যন্ত দূরত্ব হলো উচ্চতার ৪ ভাগের ১ ভাগ
- কনুই থেকে হাতের অগ্রভাগ পর্যন্ত দূরত্ব হলো উচ্চতার ৪ ভাগের ১ ভাগ (যাকে আমরা বাংলায় বলি: প্রত্যেকে যার যার হাতে সাড়ে তিন (৩.৫) হাত। দশমিক বাদ দিলে তা হয় ৪ হাত)
- কনুই থেকে বোগল পর্যন্ত দূরত্ব হলো উচ্চতার ৮ ভাগের ১ ভাগ
- সম্পূর্ণ হাতের দূরত্ব হলো উচ্চতার ১০ ভাগের ১ ভাগ
- লিঙ্গের গোড়া, মানুষের উচ্চতার প্রায় অর্ধার্ধ বরাবর অবস্থান করে
- পায়ের পাতা, মানুষের উচ্চতার ৭ ভাগের ১ ভাগ
- পায়ের তলা থেকে হাঁটুর নিচ পর্যন্ত দূরত্ব হলো উচ্চতার ৪ ভাগের ১ ভাগ
- হাঁটুর নিচ থেকে লিঙ্গের গোড়া অবধি দূরত্ব হলো উচ্চতার ৪ ভাগের ১ ভাগ
- থুতনির নিচ থেকে নাক পর্যন্ত এবং ভুরু থেকে চুলের গোড়া পর্যন্ত দূরত্ব, কান থেকে মুখমন্ডলের এক তৃতীয়াংশ পর্যন্ত দূরত্বের সমান
লিওনার্দো’র এই মনুষ্য-ছবিটি যেহেতু ভিট্রুভিয়াসের বর্ণিত অনুপাতকে উপজীব্য করে আঁকা, তাই একে ‘ভিট্রুভিয়াসের মানুষ’ বা ভিট্রুভিয়ান ম্যান’ হিসেবে ডাকা হয়।
ভিট্রুভিয়াসের অনুপাতকেন্দ্রীক হলেও ছবিটিতে লিওনার্দো ভিট্রুভিয়াসের অনেক খুঁত ঠিক করে এঁকেছেন। রেখেছেন তাঁর শিল্পকুশলতা, গণিত ও জ্যামিতি চেতনা এবং গুপ্তবিদ্যা-চর্চার স্পষ্ট ছাপ। কী সেই বিশেষ কুশলতা, তা জানার আগ্রহ আমাদেরকে নিয়ে যাবে ৮ম শতাব্দিতে।
মুহাম্মদ ইব্ন মুসা আল-‘খারিযমি (Muhammad ibn Mūsā al-Khwārizmī), হ্যা, বীজগণিতের প্রবর্তক, খারিযমি নামে যিনি সমধিক পরিচিত, তিনি বীজগণিতের একটা সমীকরণকে বর্ণনা করে তার নাম দিলেন “জিনিসটি” (the Thing), এই সমীকরণটি ছিল অমিমাংসিত। তাঁর সেই অমিমাংসিত সমীকরণের একই সূত্র নিয়ে যায় আমাদেরকে আরো বহু বহু যুগ আগে প্রাচীন গ্রিসে, গণিতবিদ ইউক্লিডের কাছে। ইউক্লিড, জ্যামিতির ভাষায় একটা সরলরেখাকে একটি বিন্দু দিয়ে দ্বিভাজিত করে আলোচনা করে গেছেন এই একই সত্য।
কী তবে এই সত্য? …এক দশমিক ছয় এক আট… 1.618…। গণিতে যাকে আদর করে ডাকা হয় ‘ফাই’, এবং প্রকাশ করা হয় গ্রিক অক্ষর φ [ফাই] দিয়ে (বৃত্ত সংশ্লিষ্ট পাই নয় কিন্তু)। এই অনুপাতটিকে সবাই ডাকে ‘সোনালি অনুপাত’ বলে। জ্যামিতিতে একে বসালে ডাকে ‘সোনালি ভগ্নাংশ’। রেনেসাঁ’র লেখকরা বলতেন ‘ঐশ্বরিক অনুপাত’ (Divine Proportion)। সোনালি ভগ্নাংশের হিসাবটা এরকম: (AC ÷ AB) = (CB ÷ AC)। যার দ্বিঘাত সমীকরণ (কুয়াড্রেটিক ইকুয়েশন) করলে মান হয় 0.618… থেকে 1.618…।
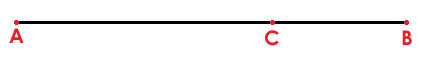
এই সোনালি অনুপাতকে প্রসিদ্ধ করেছিলেন ইতালিরই আরেক গণিতবিদ লিওনার্দো ফিবোনাক্কি (Leonardo Fibonacci), যাকে অনেকেই পিসা’র লিওনার্দো বলে ডাকতেন। তিনিই প্রথম খুঁজে দেখালেন, প্রকৃতির অনেক কিছুতেই দেখা যায় এই অনুপাত। তিনি আবিষ্কার করলেন বিখ্যাত একটি সিরিজ বা ক্রম:
0 – 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55 – …
এই ক্রমটি তাঁরই নামে ‘ফিবোনাক্কি সিরিয’ হিসেবে আজও সমাদৃত। এতে পর পর দুটো অংকের যোগফল মিলে হয় তার পরের অংকটি, এবং মজার ব্যাপার হলো এদের একটার সাথে আরেকটার ভাগফল 0.618 থেকে 1.618-এর মধ্যে উঠানামা করে।
ফিবোনাক্কিই প্রথম, ঐশ্বরিক অনুপাত খুঁজে দেখেন প্রকৃতির নানা কিছুতে। তিনি জানান, সামুদ্রিক শামুকের (nautilus) খোলসের ভিতরকার ঘূর্ণাবর্ত কক্ষগুলো একটি তার পরেরটির ফাই। মৌচাকে, পুরুষ আর নারী মৌমাছির সংখ্যানুপাত হয় ফাই। সূর্যমুখী ফুলের বীজগুলোর সারির অনুপাত হয় ফাই। পাইন ফলের ছাতাগুলোর অনুপাত হয় ফাই। উদ্ভিদের ফিলোটেক্সিস (Phyllotaxis) বা পাতার বিন্যাস তত্ত্বে এই সিরিয বা সোনালি অনুপাতের রয়েছে বিশেষ গুরুত্ব। …এখন স্বভাবতই প্রশ্ন জাগে: তাহলে মানবদেহে?
আপনার নিজের উচ্চতাটা মেপে নিন, এবারে আপনার কোমর বা কটিদেশ থেকে মেঝে পর্যন্ত উচ্চতাটা নিন। একটাকে আরেকটা দিয়ে ভাগ করুন— ফাই। হাতের কাঁধ থেকে আঙ্গুলের ডগা এবং কনুই থেকে আঙ্গুলের ডগা, ভাগ করুন— ফাই। কনুই থেকে আঙ্গুলের ডগা এবং কব্জি থেকে আঙ্গুলের ডগা— ফাই। কব্জি থেকে আঙ্গুলের ডগা এবং আঙ্গুলের গোড়া থেকে আঙ্গুলের ডগা— ফাই। আঙ্গুলের গিট থেকে…। এভাবে পায়ের ক্ষেত্রেও বিষয়টা একই।
ফাই, ফাই, ফাই — এই ফাইয়ের গুণে মুগ্ধ হয়ে লিওনার্দো’র মতোই বিখ্যাত চিত্রকর মাইকেল অ্যাঞ্জেলো, আলবাখ দুরারও তাদের চিত্রকর্মে ফাইয়ের কীর্তন করে গেছেন কখনও দৃশ্যপটে, কখনও আলোচ্য বস্তুর বিভিন্ন আঙ্গিকে। চিত্রশিল্পেই শুধু নয়, সুর জগতের কর্ণধার মোযার্ট তাঁর ফিফ্থ সিম্ফনিতে, বার্তুক, দেবুসি, শুবার্ট প্রমুখ সঙ্গীতকার তাদের সুরকর্মেও রেখে গেছেন ফাইয়ের বৈশিষ্ট্য।
এবারে একটা কাজ করা যাক: একটা স্টার, মানে তারা আঁকা যাক। সাথে সাথে আপনি কাগজ-কলম নিয়ে এইমাত্র একটানে যে তারাটা আঁকলেন, সেটি একটি পাঁচ-মাথা তারা (বেশিরভাগ ক্ষেত্রেই ব্যক্তি এই পাঁচ-মাথা তারা এঁকে থাকেন)। যদি সঠিক অনুপাতে আঁকা হয়, তাহলে দেখবেন, এই পাঁচ-মাথা তারা’র (pentacle, pentagram, five-pointed star) প্রতিটা দাগ একে অপরকে যেভাবে কাটাকুটি করেছে, তাতে কিন্তু ভাগফল আসে ফাই।
যাহোক, যেখানে শুরু, সেখানেই শেষ করা যাক: স্থাপত্য থেকে যে মনুষ্য অনুপাতের ধারণা দিয়েছিলেন ভিট্রুভিয়াস, তা যে লিওনার্দো কায়দায় আজকের ভিট্রুভিয়ান ম্যান হয়ে আমাদের সামনে এসেছে, তার পিছনে ছিল একজন মানুষের গভীর রাতে কবর থেকে লাশ তুলে নিয়ে এসে কাটাকুটি করে করা জ্যামিতি। আর সেখানে শুধু ভিট্রুভিয়াসের ধীশক্তিরই শুধু ঠাঁই হয়নি, লিওনার্দো ছবিটির পরতে পরতে রেখেছেন অনেক কিছু। ছবিটিতে [নাভিকে কেন্দ্র ধরে নিয়ে] বৃত্তটির যে ব্যাসার্ধ পাওয়া যায়, তা দিয়ে যদি বর্গক্ষেত্রের বাহুর দৈর্ঘ্যকে ভাগ করা যায়, তাহলে কী পাওয়া যাবে? আর বোধহয় বলা লাগবে না।
-মঈনুল ইসলাম


![আলোকচিত্র ০১: ঝুলন্ত সেতু শুধু রাঙামাটি নয়, মেঘলায়ও আছে [ছবি: নাকিব আহমেদ]](https://nishachor.com/wp-content/uploads/2011/05/01hangingbridge.jpg)

Nice work and congrat Mayenul – milestone blog and it is a good one too – will read with more time in hand
আপনাকেও ধন্যবাদ। 🙂
সত্যিই অসাধারণ। ধন্যবাদ মঈনুল ইসলাম। আপনার সুসজ্জিত আক্ষরিক এবং শাব্দিক বিন্যাস লেখাটিকে যথাযথ করে তুলেছে। লেখাটি পাঠকদের সহজেই অনুপ্রানিত করবে